Евклид: различия между версиями
(комментариии Туси) |
м (Птолемей) |
||
| (не показано 45 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
[[Изображение:Euclides.gif|thumb|230px|Предполагаемый облик ''Евклида'']] | [[Изображение:Euclides.gif|thumb|230px|Предполагаемый облик ''Евклида'']] | ||
| − | '''Евкли́д''' — автор первой математической книги человечества [[«Начала» Евклида|''«Начала»'']] (лат. ''«Elementa»'', греч. ''«Στοιχεῖα»''), состоящей из 13 томов, к которым позднее добавлены ещё два | + | '''Евкли́д''' — автор первой математической книги человечества [[«Начала» Евклида|''«Начала»'']] (лат. ''«Elementa»'', греч. ''«Στοιχεῖα»'' — «основания, начала, элементы, стихии»), состоящей из 13 томов, к которым позднее добавлены ещё два |
__TOC__ | __TOC__ | ||
| Строка 9: | Строка 9: | ||
''Вечный друг человечества, математик Евклид.'' | ''Вечный друг человечества, математик Евклид.'' | ||
| − | === | + | === «Начала» ''Евклида'' === |
| − | В ''«Началах»'' была предпринята первая попытка | + | В ''«Началах»'' была предпринята первая попытка аксиоматического построения геометрии,— здесь излагается, так называемый ''«синтетический»'', аксиоматически–дедуктивный, [[Научный метод|метод]] решения геометрических задач. Здесь содержатся основы элементарной геометрии, [[Арифметика|теории чисел]], методы определения площадей и объёмов простейших фигур. Этот труд оказывал огромное влияние на развитие математики вплоть до Новейшего времени — ещё в середине XIX в. он был настольной книгой школяров, и даже современное изложение школьной планиметрии во многом заимствует идеи ''Евклида''. ''«Начала»'' выдержали более 500 печатных переизданий, начиная с [[1482]] года, когда были опубликованы впервые. |
Вопреки распространённому заблуждению, термины «аксиома» (новогреческое αξιωμα «требование, желание, основное положение, исходный принцип», от греческого αξια — «достоинство, заслуга»), «постулат» (лат. ''postulatio'' — «требование, просьба, жалоба, обращение») в «Началах» Евклида не употребляются, современная классификация аксиом и постулатов ''Евклида'' была произведена ''И.Л. Гейбегером'', в его издании «Начал» [[1883]]—[[1888|88]] годов. | Вопреки распространённому заблуждению, термины «аксиома» (новогреческое αξιωμα «требование, желание, основное положение, исходный принцип», от греческого αξια — «достоинство, заслуга»), «постулат» (лат. ''postulatio'' — «требование, просьба, жалоба, обращение») в «Началах» Евклида не употребляются, современная классификация аксиом и постулатов ''Евклида'' была произведена ''И.Л. Гейбегером'', в его издании «Начал» [[1883]]—[[1888|88]] годов. | ||
| Строка 37: | Строка 37: | ||
:''«Этими письмами обменивались некоторые преподаватели школ при Кёльнском и Льежском соборах. Перед тем как отправить их адресатам, они, как правило, читали и комментировали их в соответствующих научных кругах. Из содержания писем очевидно, что эти преподаватели пытались выяснить понятия о внутренних и внешних углах треугольника. Они пришли к выводу, что внутренний угол означает острый угол, а внешний — тупой. Понятно, что в таких условиях и речи не могло быть о доказательстве теоремы о сумме углов треугольника, несмотря на то, что было известно, что она равна двум прямым углам. В этих письмах для π даётся (неизвестного происхождения) значение 25/8, ...»'' ([11, стр. 179]) | :''«Этими письмами обменивались некоторые преподаватели школ при Кёльнском и Льежском соборах. Перед тем как отправить их адресатам, они, как правило, читали и комментировали их в соответствующих научных кругах. Из содержания писем очевидно, что эти преподаватели пытались выяснить понятия о внутренних и внешних углах треугольника. Они пришли к выводу, что внутренний угол означает острый угол, а внешний — тупой. Понятно, что в таких условиях и речи не могло быть о доказательстве теоремы о сумме углов треугольника, несмотря на то, что было известно, что она равна двум прямым углам. В этих письмах для π даётся (неизвестного происхождения) значение 25/8, ...»'' ([11, стр. 179]) | ||
| − | ''Евклиду'' также приписываются и другие работы по | + | ''Евклиду'' также приписываются и другие работы по геометрии, астрономии, оптике,перспективе, логике, о свойствах зеркал, теории музыки, а также — трактат в 3–х книгах неизвестного содержания ''«Поризмы»'' (греч. ''πορισμος'' «приобретение»), который, судя по упоминаниям в «Комментарии» ''Прокла'' и в «Математическом сборнике» ''Паппа'', содержал 171 «поризму». Трактат собирался «восстановить» французский филолог, юрист и математик ''Пьер Ферма'', но не преуспел в этом, не удалось попытка восттановления геометрам ''Альберту Жирару'', ''Буало'' и ''Ренальдини''. Но в [[1723]] году ''воспроизвёл'' из неизвестных сегодня соображений шотландский математик ''Роберт Симсон''. Впрочем, в [[1837]] году французский математик ''Мишель Шаль'' предположил, что ''«Поризмы»'' должны были содержать фрагменты аналитической геометрии, и написал свой вариант этой книги. ''Шаль'' определил ''поризму'', как |
* ''«неполную теорему, выражающую известные соотношения между вещами, изменяющимися по общему закону»'' или же как | * ''«неполную теорему, выражающую известные соотношения между вещами, изменяющимися по общему закону»'' или же как | ||
* ''«предложение, в котором высказывается некоторая истина и при этом утверждается, что можно всегда найти известные вещи, эту истину дополняющие»''. | * ''«предложение, в котором высказывается некоторая истина и при этом утверждается, что можно всегда найти известные вещи, эту истину дополняющие»''. | ||
| Строка 50: | Строка 50: | ||
В [[Традиционная хронология|традиционной истории]] науки принято считать, что ''Евклид'' являлся ''«древнегреческим, [[Античность|античным]]»'' математиком. Даты его жизни приводятся разные: согласно ([1]), ''Евклид'' жил в ''«315—255 гг. до РХ»''; по сообщению ([2]), он жил ''«ок. 365 – ок. 300 гг. до н.э.»''; согласно ([10, стр. 366]), «работал в Александрии в 3 веке до н.э.». Принято также считать, что ''Евклид'' родился в Афинах и был учеником ''[[Платон]]а''. | В [[Традиционная хронология|традиционной истории]] науки принято считать, что ''Евклид'' являлся ''«древнегреческим, [[Античность|античным]]»'' математиком. Даты его жизни приводятся разные: согласно ([1]), ''Евклид'' жил в ''«315—255 гг. до РХ»''; по сообщению ([2]), он жил ''«ок. 365 – ок. 300 гг. до н.э.»''; согласно ([10, стр. 366]), «работал в Александрии в 3 веке до н.э.». Принято также считать, что ''Евклид'' родился в Афинах и был учеником ''[[Платон]]а''. | ||
| − | Но такое мнение возникло недавно и разделялось не всегда: первоиздатель ''«Начал»'' [[Ратдольт, Эргард|''Э. Ратдольт'']] считал ''Евклида'' учеником ''[[Сократ]]а'', родившемся в Мегаре. Также думал и ''[[Диоген Лаэртский]]'' — в его описании | + | Современная нам [[Традиционная хронология|традиционная]] датировка времени жизни ''Евклида'' привязана к традиционной же дате правления диадоха, царя Египта ''Птолемея I Сотера''. Поскольку неоплатоник ''Прокл Диадох'' рассказывает о диалоге математика ''Евклида'' с тем ''Птолемеем'', где ''Евклид'' высказал свой афоризм об отсутствии царского пути в изучении геометрии. |
| + | |||
| + | Но такое мнение возникло недавно и разделялось не всегда: первоиздатель ''«Начал»'' [[Ратдольт, Эргард|''Э. Ратдольт'']] считал ''Евклида'' учеником ''[[Сократ]]а'', родившемся в Мегаре. | ||
| + | |||
| + | ''Мегарским'' называли ''Евклида'' некоторые последующие издатели ''«Начал»'' — ''Бартоломео Замберти'' ([[1473]]−[[1539]]) в венецианском издании [[1505]] года; ''Лука Пачиоли'' ([[1445]]−[[1514]]) в венецианском издании [[1509]] года; ''Якоб Фабер'' ([[1455]]−[[1537]]) в парижском издании [[1516]] года; ''Николо Тарталья'' ([[1499]]−[[1557]]) в венецианском издании [[1543]] года; ''Джон Ди'' ([[1527]]−[[1608]]) в лондонском издании [[1559]] года; епископ ''Франсуа Фуа'' ([[1502]]—[[1594]]) в парижском издании [[1566]] года. | ||
| + | |||
| + | Также думал и ''[[Диоген Лаэртский]]'' — в его описании логического метода ''Евклида Мегарского'', нетрудно угадать искажённое изложение аксиоматического метода доказательств, свойственного книге [[«Начала» Евклида|«Начал» ''Евклида'']]: | ||
: ''«Оспаривая доказательства, он оспаривал в них не исходные положения, а выведение следствий. Так, он отрицал умозаключения по аналогии, потому что они опираются или на сходное, или на несходное; если на сходное, то лучше уж обращаться не к сходному, а к самому предмету, а если на несходное, то неуместно само их сопоставление.»'' ([8, 2:10]) | : ''«Оспаривая доказательства, он оспаривал в них не исходные положения, а выведение следствий. Так, он отрицал умозаключения по аналогии, потому что они опираются или на сходное, или на несходное; если на сходное, то лучше уж обращаться не к сходному, а к самому предмету, а если на несходное, то неуместно само их сопоставление.»'' ([8, 2:10]) | ||
| Строка 93: | Строка 99: | ||
[[Изображение:Euclid Maldives.gif|180px|right]] | [[Изображение:Euclid Maldives.gif|180px|right]] | ||
* первое печатное издание ''Евклида'' [[Ратдольт, Эргард|''Эргарда Ратдольта'']] ''«Opus elementorum Euclidis Megarensis in geometriam artem, in id quoque Campani commentationes»'' (Венеция, 25 мая [[1482]] г.), считающееся переводом [[Кампанус, Джованни|''Дж. Кампануса'']] ''«Начал»'' с арабского языка | * первое печатное издание ''Евклида'' [[Ратдольт, Эргард|''Эргарда Ратдольта'']] ''«Opus elementorum Euclidis Megarensis in geometriam artem, in id quoque Campani commentationes»'' (Венеция, 25 мая [[1482]] г.), считающееся переводом [[Кампанус, Джованни|''Дж. Кампануса'']] ''«Начал»'' с арабского языка | ||
| − | * якобы, перевод с греческого на латынь, издание ''Б. Цамберти'' ''«Euclidis Megarensis | + | * якобы, перевод с греческого на латынь, издание ''Б. Цамберти'' ''«Euclidis Megarensis Mathematici clarissimi Elementorum geometricorum libri XV»'' ([[Венеция]]: ''B. Zamberti'', [[1505]]) — это издание в [[1507]] г. купил для своей библиотеки [[Дюрер, Альбрехт|''А. Дюрер'']] |
| − | * итальянское исправленное издание «Начал» [[Пачоли, Лука|''Луки Пачоли'']] | + | * итальянское исправленное издание «Начал» [[Пачоли, Лука|''Луки Пачоли'']] ''«Euclidis megarensis philosophi acutissimi mathematicorumque omnium sine controversia principis opera a Campano interprete fidissimo tralata»'' [[1509]] (не сохранилось) |
| − | * первое издание на греческом ''Гринеуса'' ''«Euclidis opera cum Theonis expositione»'' (Базель, [[1533]], [[1550]]) | + | * парижское издание ''Якоба Фабера'' (он же — ''Жак Лефевр д'Эстапль'', [[1455]]—[[1537]]) ''«Geometria Euclidis Megarensis»'' ([[1516]]) |
| + | * первое издание на греческом ''Симона Гринеуса'' ''«Euclidis opera cum Theonis expositione»'' (Базель, [[1533]], [[1550]]) | ||
* первый сохранившийся итальяноский перевод «Начал» сделан ''Николо Тартальей'' в Венеции: ''«Euclide Megarense philosopho Solo introduttore delle scientie mathematice»'' в [[1543]], его исправленное издание вышло в [[1565]] году и далее до [[1586]] года вышло всего семь изданий | * первый сохранившийся итальяноский перевод «Начал» сделан ''Николо Тартальей'' в Венеции: ''«Euclide Megarense philosopho Solo introduttore delle scientie mathematice»'' в [[1543]], его исправленное издание вышло в [[1565]] году и далее до [[1586]] года вышло всего семь изданий | ||
* первые 6 книг ''«Начал»'' в переводе [[Камерарий, Иоахим|''Иоахима Камерария'']] под редакцией [[Ретик, Георг Иоахим|''Иоахима Ретика'']] ''«Elementorum geometricorum libri sex, conversi in Latinum sermonem a Ioach. Camerario»'' ([[1549]]) | * первые 6 книг ''«Начал»'' в переводе [[Камерарий, Иоахим|''Иоахима Камерария'']] под редакцией [[Ретик, Георг Иоахим|''Иоахима Ретика'']] ''«Elementorum geometricorum libri sex, conversi in Latinum sermonem a Ioach. Camerario»'' ([[1549]]) | ||
* первое издание ''«Катоптрики»'': ''«Euclidis Optica & catoptrica per Ioannem Penam regivm mathematicum, ad illvstrissimvm principem Carolvm Lotharingvm Cardinalem»'' (Parisiis: Ex officina ''Andreae Wecheli'', [[1557]]) | * первое издание ''«Катоптрики»'': ''«Euclidis Optica & catoptrica per Ioannem Penam regivm mathematicum, ad illvstrissimvm principem Carolvm Lotharingvm Cardinalem»'' (Parisiis: Ex officina ''Andreae Wecheli'', [[1557]]) | ||
| + | * первый немецкий перевод шести книг ''«Начал»'' выполненный [[Ксиландер|''Ксиландром'']]: ''«Die sechs ersten Bücher Euclidis vom Anfang oder Grund der Geometrie, in welchen der echte grund, nicht allein der Geometrie ...»'', Basel: [[1562]] | ||
| + | * парижское издание ''Франсуа Фуа'' (он же — ''Флуссатес'' граф ''де Кандалла'' епископ Эра, [[1502]]—[[1594]]) ''«Euclidis Megarensis mathematici clarissimi elementa geometrica libris XV»'' ([[1566]]), написал три книги продолжения евклидовых ''«Начал»'', опубликованные в [[1578]] и [[1602]] годах | ||
* критика Евклида в историко—математическом сочинении [[Рамус, Пьер|''Пьера Рамуса'']] ''«Р. Rami Scholarum mathematicarum libri unus et triginta»'' (Франкфурт, [[1559]]; Базель, [[1569]]) | * критика Евклида в историко—математическом сочинении [[Рамус, Пьер|''Пьера Рамуса'']] ''«Р. Rami Scholarum mathematicarum libri unus et triginta»'' (Франкфурт, [[1559]]; Базель, [[1569]]) | ||
* английское издание [[Ди, Джон|''Джона Ди'']] ''«The elements of geometrie of the most auncient Philosopher Euclide of Megara»'', перевод на английский язык ''Генри Биллингслея'' (Imprinted at London by ''Iohn Daye'', [[1559]]; [[1570]]) | * английское издание [[Ди, Джон|''Джона Ди'']] ''«The elements of geometrie of the most auncient Philosopher Euclide of Megara»'', перевод на английский язык ''Генри Биллингслея'' (Imprinted at London by ''Iohn Daye'', [[1559]]; [[1570]]) | ||
* латинский перевод 15 книг ''«Начал»'' [[Коммандино, Федериго|''Федериго Коммандино'']] ''«Euclidis Elementorum libri XV una cum scholiis antiquis»'' (Pisauri: ''Jacobus'', [[1572]]) | * латинский перевод 15 книг ''«Начал»'' [[Коммандино, Федериго|''Федериго Коммандино'']] ''«Euclidis Elementorum libri XV una cum scholiis antiquis»'' (Pisauri: ''Jacobus'', [[1572]]) | ||
* комментированное издание ''«Начал»'' ''«Euclidis elementorum libri XVI cum scholiis»'' [[Клавий|''Христофа Шлюсселя (Клавия)'']] ([[1574]]) | * комментированное издание ''«Начал»'' ''«Euclidis elementorum libri XVI cum scholiis»'' [[Клавий|''Христофа Шлюсселя (Клавия)'']] ([[1574]]) | ||
| − | * римское издание Евклида с комментариями ''Абу–Джафара Мухаммеда Насир–эд–Дина Туси'' (якобы XIII в.) '' | + | * римское издание Евклида с комментариями ''Абу–Джафара Мухаммеда Насир–эд–Дина Туси'' (якобы XIII в.) ''«Nasiridinus Tusinus. Euclidis Elementorum geometricorum libri XIII arabice impressi»'' ([[1594]]); латинский перевод — Рим, [[1657]] |
* на китайском языке первые 6 книг ''«Начал»'' издал [[Риччи, Матео|''Матео Риччи'']] во время своей миссии в [[Китай|Китае]] ([[1583]]—[[1610]]) | * на китайском языке первые 6 книг ''«Начал»'' издал [[Риччи, Матео|''Матео Риччи'']] во время своей миссии в [[Китай|Китае]] ([[1583]]—[[1610]]) | ||
| + | * оксфордские лекции сэра ''Генри Савиля'' ''«Рraelectiones tresdecim in principium elementorum Euclidis Oxonii habitae MDCXX»'' ([[1621]]) | ||
* на латинском '''«Data»''' ([[1625]]) | * на латинском '''«Data»''' ([[1625]]) | ||
| + | * первый французский перевод 15 книг ''«Начал»'' ''Евклида'', выполненный ''Дени Энрионом'' ''«Les quinze livres des éléments géométriques d'Euclide plus le livre des donnez du mesme Euclide aussi traduict en françois par ledit Henrion, et imprimé de son vivant traduction de Denis Henrion»'' (Париж, [[1632]]) | ||
| + | * антверпенское издание ''Клода Ришара'' ''«Euclidis elementorum geoinetricorum libros XIII, Isidorum et Hypsiclem et recentiores de corporibus regularibus et Procli propositiones geometricas»'' ([[1645]]) | ||
| + | * лондонское издание ''Исаака Барроу'' ''«Euclidis elementorum libri XV breviter demonstrati»'' ([[1659]]—[[1678]]) | ||
* на греческом и латинском «Euclidis quae supersunt omnia» (Оксфорд, [[1703]]) | * на греческом и латинском «Euclidis quae supersunt omnia» (Оксфорд, [[1703]]) | ||
* восстановление ''«Поризм»'' ''Евклида'' [[Симсон, Роберт|''Робертом Симсоном'']] ''"Two general propositions of Pappus, in which many of Euclid's porisms are included"'' (Глазго, [[1723]]) | * восстановление ''«Поризм»'' ''Евклида'' [[Симсон, Роберт|''Робертом Симсоном'']] ''"Two general propositions of Pappus, in which many of Euclid's porisms are included"'' (Глазго, [[1723]]) | ||
| Строка 122: | Строка 135: | ||
* ''«Евклидовых Начал осемь книг, содержащие в себе основания геометрии»'', перевод с греческого ''Фомы Ивановича Петрушевского'' (СПб, [[1819]]) | * ''«Евклидовых Начал осемь книг, содержащие в себе основания геометрии»'', перевод с греческого ''Фомы Ивановича Петрушевского'' (СПб, [[1819]]) | ||
* ''«Евклидовых Начал три книги: седьмая, осьмая и девятая, содержащие общую теорию чисел древних геометров»'', перевод с греческого ''Фомы Ивановича Петрушевского'' (СПб, [[1835]]) | * ''«Евклидовых Начал три книги: седьмая, осьмая и девятая, содержащие общую теорию чисел древних геометров»'', перевод с греческого ''Фомы Ивановича Петрушевского'' (СПб, [[1835]]) | ||
| − | * ''«Начала Евклида с пояснительным введением и толкованиями»'', вольный перевод, возможно, с латинского издания ''Р. Симсона'' [[1723]] года, ''Михаила Егоровича Ващенко–Захарченко'', опущены арифметические книги VII–IX, а во введении изложена неевклидова геометрия (Киев, | + | * ''«Восемь книг геометрии Эвклида. Переведено с немецкого издания доктора Гартвига воспитанниками Александровского Кременчугского реального училища Немировским и Бергером, под руководством Директора училища»'' (Кременчуг: типография Германа Розенталя, [[1877]]) |
| + | * ''«Начала Евклида с пояснительным введением и толкованиями»'', вольный перевод, возможно, с латинского издания ''Р. Симсона'' [[1723]] года, ''Михаила Егоровича Ващенко–Захарченко'', опущены арифметические книги VII–IX, а во введении изложена неевклидова геометрия (Киев, [[1880]]) | ||
* ''«Начала Евклида»'', перевод с греческого ''Дмитрия Дмитриевича Мордухай–Болтовского'' (Москва–Ленинград, книги I–VI — [[1948]]; книги VII–X — [[1949]]; книги XI–XV — [[1950]]) | * ''«Начала Евклида»'', перевод с греческого ''Дмитрия Дмитриевича Мордухай–Болтовского'' (Москва–Ленинград, книги I–VI — [[1948]]; книги VII–X — [[1949]]; книги XI–XV — [[1950]]) | ||
| + | |||
| + | === Продолжатели ''Евклида'' === | ||
| + | |||
| + | Несколько математических проектов прямо указывают на свою связь с замыслом «Начал» математики ''Евклида'': | ||
| + | * [[«Принципы» Ньютона|«Математические начала натуральной философии»]] («Philosophiae Naturalis Principia Mathematica», [[1686]]) англичанина [[Ньютон, Исаак|''Исаака Ньютона'']] | ||
| + | * «Начала геометрии» («Éléments de géométrie», 12 исправленных изданий, [[1794]]—[[1823]]) француза ''А.–М. Лежандра'' | ||
| + | * «О началах геометрии» ([[1829]]—[[1830]]) и «Новые начала геометрии с полной теорией параллельных линий» ([[1835]]—[[1838]]) россиянина [[Лобачевский, Николай Иванович|''Н.И. Лобачевского'']] | ||
| + | * «Основные законы арифметики» («Grundgesetze der Arithmetik: eine logisch–mathematische Untersuchung über den Begriff der Zahl», [[1884]]) немца ''Г. Фреге'' | ||
| + | * [http://ilib.mccme.ru/djvu/geometry/osn_geom.htm «Основания геометрии»] («Grundlagen der Geometrie», [[1899]]) немца ''Д. Гильберта'' | ||
| + | * «Принципы математики» ([https://plato.stanford.edu/entries/principia-mathematica/ «Principia Mathematica»], [[1910]]—[[1913]]) англичан ''А.Н. Уайтхеда'' и ''Б. Рассела'' | ||
| + | * [http://www.px-pict.com/9/6/2/8/2.html «Основания математики»] («Grundlagen der Mathematik», [[1934]]—[[1939]]) немца ''Д. Гильберта'' и швейцарца ''П. Бернайса'' | ||
| + | * «Элементы математики» («Éléments de mathématique», [[1939]]—[[2016]]) французов ''Н. Бурбаки'' | ||
| + | * «Основания алгебраической геометрии» («Éléments de Géométrie Algébrique», ÉGA, [[1960]]—[[1967]]) космополита [http://math.ivanovo.ac.ru/school/solon/grot.html ''А. Гротендика''] и француза ''Ж. Дьедонне'' | ||
| + | |||
| + | === Мнения и анекдоты === | ||
| + | |||
| + | : ''«... по отношению к сочинениям гуманитарного характера мы можем либо прямо указать предполагаемого автора, либо, по крайней мере, очертить круг людей, вполне способных им быть по их образованию, культуре и литературному дарованию. Совсем иначе дело обстоит, скажем, с Евклидом. Кто из ученых средневековья мог бы претендовать на эту роль? Вот что пишет по этому поводу [[Морозов, Николай Александрович|Морозов]]: «Учёный, переписывая с дополнениями книгу дня себя, писал на ней совершенно справедливо то имя. которым она была помечена до него. «Геометрия Евклида», — отмечал он, — умолчав о том, что сам прибавил две–три теоремы от себя и лучше обосновал ту или другую из старых. Так он давал повод и последующему копиисту своей рукописи добавить две-три теоремы, сохранив за учебником прежнее имя. И вот, с течением веков, небольшой десяток теорем, который мог действительно быть собранным человеком этого имени (имя Евклид значит — хорошо одетый), превращался в большую и хорошо развитую во всех своих деталях книгу. А последующий учёный, упустивший из виду этот вековой процесс улучшения, начинал приписывать все такое коллективное творчество одному древнему гиганту геометрической науки и вместе с тем определять ложно высокий уровень познания в очень древние времена. На деле же вся книга представляла сумму познаний целого исторического периода до тех пор, когда печатный станок впервые повсюду распространил её и указал время и место её первого издания» ([[«Христос» Н.А. Морозова|«Христос»]], Т. 4.— М–Л.: ГИЗ, [[1928]], стр. 174–175). Добавим, что «Евклид» может означать также «хорошо переплетённый». Описанный механизм бессознательного коллективного творчества хорошо объясняет происхождение таких всеобъемлющих трактатов, как «Альмагест» Птолемея или «Начала» Евклида, и тот факт, что ссылки на них были возможны задолго до окончательного оформления их текста. Он не предполагает никакого явного обмана и мистификационных устремлений со стороны авторов и издателей, хотя возможность эта отнюдь не может быть исключена. Вместе с тем правила издания «древних» текстов были на заре книгопечатания явно отличны от современных. Как показывает пример, скажем, «Альмагеста», редакторы и издатели окончательного текста, не колеблясь, вносили в него поправки и дополнения, соответствующие последнему слову науки, никак это специально не оговаривая. Не потому ли «переводу» научных книг часто предшествовал «дурной перевод», не содержащий этих поправок и отражающий предыдущий этап развития науки?»'' (М.М. Постников «Критическое исследование хронологии древнего мира. I т.», §4) | ||
| + | |||
| + | : ''«О Эвклиде нам известно чуть больше, чем о [[Гомер]]е. Он родился в Александрии около 325 года до Р. Х. и умер около 265 года до Р. Х. Сказав это, я с неудовольствием чувствую, что мне тут же надо бы взять свои слова назад. Идея, согласно которой Эвклид действительно существовал и был единственным автором «Начал»,— это только одна из трёх теорий. Вторая состоит в том, что он существовал, но не писал «Начала» — по крайней мере не писал их сам. Он мог возглавлять группу математиков, создавших «Начала» коллективно. Суть третьей теории — более спорной, но всё ещё лежащей в рамках возможного — в том, что такая группа существовала, но сильно смахивала на группу математиков — по бóльшей части французов и по бóльшей части молодых,— писавших в середине двадцатого столетия под именем Николя Бурбаки. Так что «Эвклид» может оказаться коллективным псевдонимом. Тем не менее наиболее убедительная версия, похоже, состоит в том, что Эвклид всё же существовал и что это был один человек, который сам и написал «Начала». Это не означает, что Эвклид сам открыл всё математическое содержание, которое вы найдёте на страницах его книги. ...»'' (И. Стюарт «Истина и красота: Всемирная история симметрии»,— М.: Астрель: CORPUS, [[2010]], стр. 47) | ||
| + | |||
| + | В историко–математическом сочинении «Eléments d'histoire des mathématiques» [[1960]] года ''Н. Бурбаки'' (основным автором текста, по–видимому, был ''Ж.А.Э. Дьедонне'', [[1906]]—[[1992]]) написали об истинных создателях «Начал» ''Евклида'' — математиках XV—XVII вв., а также их работе, следующее: | ||
| + | |||
| + | : ''«При таком взгляде на математику аксиомы не подвергались сомнению и не обсуждались, так же как и правила вывода; единственное, что предоставлялось каждому исследователю в зависимости от его склонности, это право либо рассуждать «по образцу древних», либо дать свободу своей интуиции. Выбор точки отправления также зависел от индивидуального вкуса, в результате чего появляются многочисленные «издания» Евклида, в которых самым странным образом искажена прочно сработанная логика «Начал»;...»'' («Очерки по истории математики»,— М.: КомКнига, [[2007]], стр. 22) | ||
| + | |||
| + | Американский математик ''Роберт Рот Столл'' (''Robert Roth Stoll'', [[1915]]—[[1991]], выпускник Йельского университета, США, [[1943]]) в учебнике для студентов Оберлинского колледжа «Sets, logic, and axiomatic theories» ([[1961]]) изложил своё ошибочное понимание логического строения «Начал» ''Евклида'' (цитирование по русскому переводу этой книги): | ||
| + | |||
| + | : ''««Начала» построены следующим образом. Сначала даются определения (по всей вероятности, считавшиеся ''Евклидом'' удовлетворительными) некоторых ''первичных терминов'', таких, как ''точка'', ''прямая'' и ''плоскость''. Затем описываются различные свойства этих первичных терминов (некоторые из этих описаний ''Евклид'' называл ''аксиомами'', другие — ''постулатами''). Очевидно, утверждение о наличии этих свойств воспринимались как истинные на основании смысла предложенных определений рассматриваемых терминов. Далее, с помощью первичных терминов определялись некоторые другие понятия, а из аксиом и постулатов выводидись логическим путём описания новых свойств, называемые ''теоремами''.»'' (''Столл Р.Р.'' «Множества. Логика. Аксиоматические теории»,— М.: Просвещение, [[1968]], стр. 139–140) | ||
| + | |||
| + | Французский популяризатор математики [https://www.youtube.com/user/Micmaths ''Микаэль Лонэ''] в книге [https://www.ozon.ru/context/detail/id/145059954/ «Большой роман о математике»] ([https://www.amazon.fr/s/ref=dp_byline_sr_book_1?ie=UTF8&text=Mickael+Launay&search-alias=books-fr&field-author=Mickael+Launay&sort=relevancerank ''Mickaël Launay''] «Le grand roman des maths: De la préhistoire à nos jours») сообщает своё мнение об ''Евклиде'': | ||
| + | |||
| + | : ''«О жизни ''Евклида'' не сохранилось такого большого количества информации, как о ''Фалесе'' или ''Пифагоре''. По одним данным, он жил где–то в районе Александрии. По другим — по аналогии с ''Пифагором'', некоторые историки предполагают, что это вымышленное имя, под которым скрывается наследие нескольких учёных. Наверняка это нельзя определить.»'' (стр. 84) | ||
=== См. также === | === См. также === | ||
| + | * [[Коммандино, Федериго]] | ||
| + | * [[Ксиландер]] | ||
* [[Ратдольт, Эргард]] | * [[Ратдольт, Эргард]] | ||
| − | |||
* [[Ретик, Георг Иоахим]] | * [[Ретик, Георг Иоахим]] | ||
* [[Риччи, Матео]] | * [[Риччи, Матео]] | ||
| Строка 144: | Строка 190: | ||
# Кымпан Ф. ''«История числа π»'',— М.: Наука, [[1971]], 216 с. | # Кымпан Ф. ''«История числа π»'',— М.: Наука, [[1971]], 216 с. | ||
# Folkerts M. [http://www.math.ubc.ca/~cass/Euclid/folkerts/folkerts.html ''«Euclid in Medieval Europe»''],— München, [[1989]] | # Folkerts M. [http://www.math.ubc.ca/~cass/Euclid/folkerts/folkerts.html ''«Euclid in Medieval Europe»''],— München, [[1989]] | ||
| + | # [[Постников, Михаил Михайлович|Постников М.М.]] «Критическое исследование хронологии древнего мира. В 3–х томах»,— М.: Крафт+Леан, [[2000]] (написана в [[1978]]), 448+400+400 сс. | ||
| + | # Стюарт И. ''«Истина и красота: Всемирная история симметрии»'',— М.: Астрель: CORPUS, [[2010]], 461 с. | ||
==Ссылки== | ==Ссылки== | ||
| Строка 150: | Строка 198: | ||
* ''Рыбников К.А'' [http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=rm&paperid=8809&option_lang=rus Русские издания «Начал» Евклида (библиографические заметки)] // Успехи Математических Наук, [[1941]], вып. 9, с. 318–321 | * ''Рыбников К.А'' [http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=rm&paperid=8809&option_lang=rus Русские издания «Начал» Евклида (библиографические заметки)] // Успехи Математических Наук, [[1941]], вып. 9, с. 318–321 | ||
* [http://nausikaa2.rz-berlin.mpg.de/digitallibrary/digilib.jsp?fn=/permanent/archimedes/eucli_eleme_Z00_el_888&pn=12&ws=1&mk=0.393/0.5966&ww=1&wh=1 ''«Euclidis Codex»'' на греческом языке], Bodleiana Bibliotheca | * [http://nausikaa2.rz-berlin.mpg.de/digitallibrary/digilib.jsp?fn=/permanent/archimedes/eucli_eleme_Z00_el_888&pn=12&ws=1&mk=0.393/0.5966&ww=1&wh=1 ''«Euclidis Codex»'' на греческом языке], Bodleiana Bibliotheca | ||
| − | * [ | + | * [https://www.youtube.com/watch?v=XSvQ4gQigk4 Видеолекция профессора РАН ''А.И. Буфетова'' об ''Евклиде'' и ''Лобачевском''] |
| − | |||
Текущая версия на 17:50, 23 апреля 2024
Евкли́д — автор первой математической книги человечества «Начала» (лат. «Elementa», греч. «Στοιχεῖα» — «основания, начала, элементы, стихии»), состоящей из 13 томов, к которым позднее добавлены ещё два
Содержание
С высоты поднебесной ментальных орбит Прилетел удивительный и учёный болид. Над Землёю оставил точных знаний флюид Вечный друг человечества, математик Евклид.
«Начала» Евклида
В «Началах» была предпринята первая попытка аксиоматического построения геометрии,— здесь излагается, так называемый «синтетический», аксиоматически–дедуктивный, метод решения геометрических задач. Здесь содержатся основы элементарной геометрии, теории чисел, методы определения площадей и объёмов простейших фигур. Этот труд оказывал огромное влияние на развитие математики вплоть до Новейшего времени — ещё в середине XIX в. он был настольной книгой школяров, и даже современное изложение школьной планиметрии во многом заимствует идеи Евклида. «Начала» выдержали более 500 печатных переизданий, начиная с 1482 года, когда были опубликованы впервые.
Вопреки распространённому заблуждению, термины «аксиома» (новогреческое αξιωμα «требование, желание, основное положение, исходный принцип», от греческого αξια — «достоинство, заслуга»), «постулат» (лат. postulatio — «требование, просьба, жалоба, обращение») в «Началах» Евклида не употребляются, современная классификация аксиом и постулатов Евклида была произведена И.Л. Гейбегером, в его издании «Начал» 1883—88 годов.
Первым комментатором Евклида считают афинского неоплатоника Прокла Диадоха, жившего, будто бы в V в. н.э., оставившего замечания к первой книге «Начал». Они были обнаружены и опубликованы в Базеле по–гречески Гринеусом в 1533 году.
Как на комментатора «Начал» Евклида также указывают на Паппа Александрийского, жившего якобы в III в. н.э., некоторые его математические теоремы были опубликованы Коммандино в 1566 году, а после смерти Коммандино, в 1602 году опубликовано полное «Математическое собрание Паппа Александрийского с комментариями Коммандино».
Публикатором «Начал» Евклида считают заведующего Александрийской библиотекой Теона Александрийского, жившего якобы в конце IV в. н.э. При этом часто пишут об «издании Евклида» в редакции Теона, по всей видимости имея в виду базельское греческое издание «Euclidis opera cum Theonis expositione» 1533 года.
Утверждают, что какие–то отрывки «Начал» обнаружены при раскопках в Египте и Геркулануме.
Древнейшей рукописью «Начал» Евклида считают греческий текст, якобы 888 года, сделанный монахом Стефаном для архиепископа Цезарейского. Много греческих рукописей «Начал» относят в византийскому Средневековью, будто бы они копируют «издание» Теона Александрийского, но скорее всего, являются рукописными копиями греческого печатного текста «Начал» 1533 года.
Затем, считается, что византийские рукописи «Начал» Евклида были переведены на арабский язык и комментировались в многочисленных вариантах (Абу Юсуф Якуб Бен Исхак аль–Кинди, якобы в IX в. н.э.; Абу Наср Мухаммад ибн Мухаммад аль–Фараби, якобы в X в. н.э.; Гийяс Аддин Абу–ль–фатх Омар ибн Ибрагим аль–Хайям Нишапури, якобы в XII в. н.э.; Насир–Эддин Мерагский (Абу–Джафар Мухаммед ибн—Гасан аль–Тузи), якобы в XIII в. н.э.).
Эти арабские рукописи, известные только по упоминаниям в европейских энциклопедиях, будто бы переводились средневековыми европейскими учёными (Герардом Кремонским, якобы в XII в. н.э., Джованни Кампано, якобы в XIII в. н.э.) на латинский язык, и с этих текстов осуществлялись типографские публикации «Начал» эпохи Возрождения.
Другие работы Евклида и их судьба
Румынская историк математики Флориция Кымпан сообщает, что содержание евклидовых «Начал» стало совершенно забыто в Средневековье. Читая Евклида, европейские математики не понимали смысла употребляемых геометрических терминов. Честь «восстановления» некоторых понятий элементарной геометрии приписывается льежскому магистру Франкону (якобы XI в. н.э.):
- «Понятие о внешних и внутренних углах треугольника было совсем забыто в X–XII вв. Заслуга Франкона состоит в том, что он постиг суть понятия о внутреннем угле. Что касается внешнего угла, то он ошибался. ...» ([11, стр. 180])
Тем не менее, не понимая смысла основных рассуждений Евклида, средневековые учёные копировали его тома и обменивались письмами по его поводу (их переписка столетиями заботливо сохранялась для историков XIX века):
- «Этими письмами обменивались некоторые преподаватели школ при Кёльнском и Льежском соборах. Перед тем как отправить их адресатам, они, как правило, читали и комментировали их в соответствующих научных кругах. Из содержания писем очевидно, что эти преподаватели пытались выяснить понятия о внутренних и внешних углах треугольника. Они пришли к выводу, что внутренний угол означает острый угол, а внешний — тупой. Понятно, что в таких условиях и речи не могло быть о доказательстве теоремы о сумме углов треугольника, несмотря на то, что было известно, что она равна двум прямым углам. В этих письмах для π даётся (неизвестного происхождения) значение 25/8, ...» ([11, стр. 179])
Евклиду также приписываются и другие работы по геометрии, астрономии, оптике,перспективе, логике, о свойствах зеркал, теории музыки, а также — трактат в 3–х книгах неизвестного содержания «Поризмы» (греч. πορισμος «приобретение»), который, судя по упоминаниям в «Комментарии» Прокла и в «Математическом сборнике» Паппа, содержал 171 «поризму». Трактат собирался «восстановить» французский филолог, юрист и математик Пьер Ферма, но не преуспел в этом, не удалось попытка восттановления геометрам Альберту Жирару, Буало и Ренальдини. Но в 1723 году воспроизвёл из неизвестных сегодня соображений шотландский математик Роберт Симсон. Впрочем, в 1837 году французский математик Мишель Шаль предположил, что «Поризмы» должны были содержать фрагменты аналитической геометрии, и написал свой вариант этой книги. Шаль определил поризму, как
- «неполную теорему, выражающую известные соотношения между вещами, изменяющимися по общему закону» или же как
- «предложение, в котором высказывается некоторая истина и при этом утверждается, что можно всегда найти известные вещи, эту истину дополняющие».
Пример евклидовой поризмы, по Шалю:
- «В гиперболе произведение отрезков, образуемых касательной на асимптотах, есть величина постоянная».
В 1935 году группа английских астрономов назвала в честь Евклида кратер на видимой стороне Луны диаметром 11 км (7.4°S 29.5°W).
Когда жил Евклид?
В традиционной истории науки принято считать, что Евклид являлся «древнегреческим, античным» математиком. Даты его жизни приводятся разные: согласно ([1]), Евклид жил в «315—255 гг. до РХ»; по сообщению ([2]), он жил «ок. 365 – ок. 300 гг. до н.э.»; согласно ([10, стр. 366]), «работал в Александрии в 3 веке до н.э.». Принято также считать, что Евклид родился в Афинах и был учеником Платона.
Современная нам традиционная датировка времени жизни Евклида привязана к традиционной же дате правления диадоха, царя Египта Птолемея I Сотера. Поскольку неоплатоник Прокл Диадох рассказывает о диалоге математика Евклида с тем Птолемеем, где Евклид высказал свой афоризм об отсутствии царского пути в изучении геометрии.
Но такое мнение возникло недавно и разделялось не всегда: первоиздатель «Начал» Э. Ратдольт считал Евклида учеником Сократа, родившемся в Мегаре.
Мегарским называли Евклида некоторые последующие издатели «Начал» — Бартоломео Замберти (1473−1539) в венецианском издании 1505 года; Лука Пачиоли (1445−1514) в венецианском издании 1509 года; Якоб Фабер (1455−1537) в парижском издании 1516 года; Николо Тарталья (1499−1557) в венецианском издании 1543 года; Джон Ди (1527−1608) в лондонском издании 1559 года; епископ Франсуа Фуа (1502—1594) в парижском издании 1566 года.
Также думал и Диоген Лаэртский — в его описании логического метода Евклида Мегарского, нетрудно угадать искажённое изложение аксиоматического метода доказательств, свойственного книге «Начал» Евклида:
- «Оспаривая доказательства, он оспаривал в них не исходные положения, а выведение следствий. Так, он отрицал умозаключения по аналогии, потому что они опираются или на сходное, или на несходное; если на сходное, то лучше уж обращаться не к сходному, а к самому предмету, а если на несходное, то неуместно само их сопоставление.» ([8, 2:10])
Сообщают также, что в одной из арабских рукописей, якобы XII века, указано происхождение Евклида:
- «Эвклид, сын Наукрата, сына Зенарха, известный под именем «Геометра», учёный старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира.»
В 3 главе «О науке о звездах и познаниях астролога в этой науке» книги Низами Арузи Самарканди «Собрание редкостей, или Четыре беседы» (якобы 1156—1157 годов, впервые опубликованной в 1887–8 годах), сказано, что основы геометрии содержатся в книге Ивклида–Плотника (Иклидус–и–Наджжар), которую затем переработал Сабит ибн Курра (якобы багдадский математик IX века). Низами Арузи (с персидского — «Порядок стихосложения») упоминает Омара Хайама и других арабских учёных, открытых лишь в XIX веке, что позволяет предположить его позднее составление. В связи с этим интересно превращение Евклида Платоника (каковым он стал к XIX веку, перестав быть «Сократиком») в «Плотника», которое возможно лишь на основе русского языка.
Согласно Новой Хронологии, Евклид является фантомом традиционной истории. В книге [3, стр. 428] обосновывается гипотеза о том, что имя Евклид было одним из прозвищ Андроника I Комнина, византийского императора (якобы, 1183–1185), бывшего прототипом евангельского Иисуса. Об этом указывает сообщение Никиты Хониата, который отводит «евклидовым событиям» узкий промежуток времени между правлением императора Мануила I Комнина (якобы, 1143–1180) и первым правлением императора Исаака II Ангела (якобы, 1185–1195), когда правили малолетний Алексей II Комнин (якобы, 1180–1183) и Андроник I Комнин (якобы, 1183–1185):
- «Итак, он отправил прежде к императору Исааку (тогда еще не лишенному престола) послов с целью изложить причины явно беспричинного раздора. ... Затем он исчислял, с увеличением надлежащего веса, все огорчения своего отца, не только недавние, но и те, с которыми боролся его отец давно, когда ловкою политикой царя Мануила был оттолкнут от древнего Рима и вместе изгнан из всей Италии. Бесцеремонно поднимая эти доевклидовские события , он хотел, чтобы римляне или купили у него мир за огромную сумму денег, или не жаловались, если он немедленно начнет с ними войну.» ([4, стр. 137])
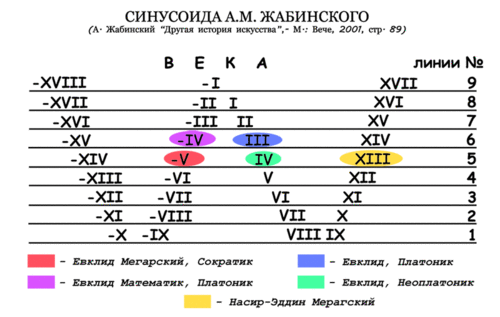
По всей видимости, математик Евклид жил на полторы тысячелетия позднее, чем считают историки: скорее всего в конце XIV века — середине XV века н.э., незадолго до того, как его «Начала» вызвали интерес в западноевропейской науке и появились его переводы.
Евклид попадает на синусоиду А.М. Жабинского, иллюстрирующую характер дублирования этого фантомного персонажа. И датировка его по «синусоиде А.М. Жабинского» указывает на XIV век н.э.
Фантомы Евклида
- Эвклид Мегарский, философ — основатель мегарской школы, ученик Сократа, учитель Эвбулида и, может быть, Стильпона и Пасикла, якобы V—IV в. до н.э.
- Эвклид, математик — якобы 315–255 до Р.Х.
- Эвклид Неоплатоник — философ, ученик Ямвлиха; упоминается в письмах императора Юлиана, якобы IV в. н.э.
- Эвклид Платоник — философ; по словам Лонгина и Прокла, писал комментарии на сочинения Платона, якобы II—III в. н.э.
- Насир–Эддин (Абу–Джафар Мухаммед ибн–Гасан аль–Тузи) — арабский математик и астроном, якобы 1201—1274, перевёл с комментариями на арабский 13 томов «Начал» Евклида, впервые опубликованную в Риме, в 1594, и, как выяснил азербайджанский астроном Габиб Джафарович Мамедбейли в 1950–х, построил обсерваторию в Мераге на территории нынешнего Южного Азербайджана
- Андроник I Комнин, византийский император (якобы, 1183—1185), бывший прототипом евангельского Иисуса
Одним из авторов работ Евклида видимо являлся францисканский монах и учёный Л. Пачоли (1445—1517), опубликовавший в 1494 г. в Венеции первую печатную книгу по геометрии «Summa de arithmetica, geometria, proportioni et proportionalita», которая пересекается по содержанию с первыми шестью книгами «Начал» Евклида, но с меньшим числом доказательств. Лука Пачоли в 1509 году издал итальянский перевод «Начал» Евклида под следующим заголовком:
- «Сочинения мегарянина Евклида, тончайшего философа и по справедливости первого из всех математиков, переведённые достойным внимания Кампано. Сочинения эти по вине издателя были настолько искажены ошибками, что едва ли в них можно узнать Евклида. Пачоли, заслуженный теолог, сей высший и редчайший между математическими науками предмет по своему разумению исправил и издал.»
Как звали Евклида?
Интересной проблемой является имя Евклида. Известно, что он упомянут у Цицерона, как «Euclides» — по-латински это слово ничего не означает. На греческом же языке его имя толкуют по-разному:
- от слова ευκλεια — «добрая слава»
- от слова ευκληις — «хорошо запертый»
- иногда приводят версию, что евклид — это «хорошо одетый» или «хорошо переплетённый»
- в имени Евклида можно найти русский корень «уклад», в таком случае название главного труда «Евклид: Начала» может быть понято как «Уложение начал»
Традиционные историки науки принимают первую версию, профессор М.М. Постников склонялся к третей, а издатель и комментатор «Начал» Евклида, иезуит Х. Шлюссель (1537—1612) считал, что смысл отражает вторая версия, и именно поэтому он взял себе псевдоним Шлюссель–Клавий (от немецкого schlüssel и латинского clavis — «ключ, отмычка»). Самого Клавия называли «Евклидом XVI века».
Все эти версии свидетельствуют о том, что Евклид — либо коллективное прозвище авторов «Начал», либо даже название самой книги («Хорошо переплетённая»). Настоящее же имя первого Евклида, данное ему при рождении, сокрыто мраком традиционной истории.
Первоиздания книг Евклида
- первое печатное издание Евклида Эргарда Ратдольта «Opus elementorum Euclidis Megarensis in geometriam artem, in id quoque Campani commentationes» (Венеция, 25 мая 1482 г.), считающееся переводом Дж. Кампануса «Начал» с арабского языка
- якобы, перевод с греческого на латынь, издание Б. Цамберти «Euclidis Megarensis Mathematici clarissimi Elementorum geometricorum libri XV» (Венеция: B. Zamberti, 1505) — это издание в 1507 г. купил для своей библиотеки А. Дюрер
- итальянское исправленное издание «Начал» Луки Пачоли «Euclidis megarensis philosophi acutissimi mathematicorumque omnium sine controversia principis opera a Campano interprete fidissimo tralata» 1509 (не сохранилось)
- парижское издание Якоба Фабера (он же — Жак Лефевр д'Эстапль, 1455—1537) «Geometria Euclidis Megarensis» (1516)
- первое издание на греческом Симона Гринеуса «Euclidis opera cum Theonis expositione» (Базель, 1533, 1550)
- первый сохранившийся итальяноский перевод «Начал» сделан Николо Тартальей в Венеции: «Euclide Megarense philosopho Solo introduttore delle scientie mathematice» в 1543, его исправленное издание вышло в 1565 году и далее до 1586 года вышло всего семь изданий
- первые 6 книг «Начал» в переводе Иоахима Камерария под редакцией Иоахима Ретика «Elementorum geometricorum libri sex, conversi in Latinum sermonem a Ioach. Camerario» (1549)
- первое издание «Катоптрики»: «Euclidis Optica & catoptrica per Ioannem Penam regivm mathematicum, ad illvstrissimvm principem Carolvm Lotharingvm Cardinalem» (Parisiis: Ex officina Andreae Wecheli, 1557)
- первый немецкий перевод шести книг «Начал» выполненный Ксиландром: «Die sechs ersten Bücher Euclidis vom Anfang oder Grund der Geometrie, in welchen der echte grund, nicht allein der Geometrie ...», Basel: 1562
- парижское издание Франсуа Фуа (он же — Флуссатес граф де Кандалла епископ Эра, 1502—1594) «Euclidis Megarensis mathematici clarissimi elementa geometrica libris XV» (1566), написал три книги продолжения евклидовых «Начал», опубликованные в 1578 и 1602 годах
- критика Евклида в историко—математическом сочинении Пьера Рамуса «Р. Rami Scholarum mathematicarum libri unus et triginta» (Франкфурт, 1559; Базель, 1569)
- английское издание Джона Ди «The elements of geometrie of the most auncient Philosopher Euclide of Megara», перевод на английский язык Генри Биллингслея (Imprinted at London by Iohn Daye, 1559; 1570)
- латинский перевод 15 книг «Начал» Федериго Коммандино «Euclidis Elementorum libri XV una cum scholiis antiquis» (Pisauri: Jacobus, 1572)
- комментированное издание «Начал» «Euclidis elementorum libri XVI cum scholiis» Христофа Шлюсселя (Клавия) (1574)
- римское издание Евклида с комментариями Абу–Джафара Мухаммеда Насир–эд–Дина Туси (якобы XIII в.) «Nasiridinus Tusinus. Euclidis Elementorum geometricorum libri XIII arabice impressi» (1594); латинский перевод — Рим, 1657
- на китайском языке первые 6 книг «Начал» издал Матео Риччи во время своей миссии в Китае (1583—1610)
- оксфордские лекции сэра Генри Савиля «Рraelectiones tresdecim in principium elementorum Euclidis Oxonii habitae MDCXX» (1621)
- на латинском «Data» (1625)
- первый французский перевод 15 книг «Начал» Евклида, выполненный Дени Энрионом «Les quinze livres des éléments géométriques d'Euclide plus le livre des donnez du mesme Euclide aussi traduict en françois par ledit Henrion, et imprimé de son vivant traduction de Denis Henrion» (Париж, 1632)
- антверпенское издание Клода Ришара «Euclidis elementorum geoinetricorum libros XIII, Isidorum et Hypsiclem et recentiores de corporibus regularibus et Procli propositiones geometricas» (1645)
- лондонское издание Исаака Барроу «Euclidis elementorum libri XV breviter demonstrati» (1659—1678)
- на греческом и латинском «Euclidis quae supersunt omnia» (Оксфорд, 1703)
- восстановление «Поризм» Евклида Робертом Симсоном "Two general propositions of Pappus, in which many of Euclid's porisms are included" (Глазго, 1723)
- на русском «Эвклидовы элементы, из двенадцати нефтоновых книг выбранные, и в осьмь книг чрез профессора мафематики Андрея Фархварсона сокращенныя», перевёл с латинского Иван Петрович Сатаров (СПб, 1739)
- учебник Р. Симсона "The Elements of Euclid" (1756)
- первое издание издание Евклида на еврейском языке «םודילקא רפם» или «םידומל תישאר» («Решит Лиммудим гу Сефер Иклидес») с четырьмя таблицами чертежей Авраама бен-Иосифа бен–Симона Минца с примечаниями Меира Фюртского (Берлин, 1775)
- перевод первых 6 книг «Элементов» Евклида «םדילקא» Баруха Шика (Шкловского) по предложению Виленского гаона раби Илии (Гаага, 1780)
- восстановление «Поризм» Евклида Мишелем Шалем «Les trois livres de porismes d'Euclide, rétablis pour la première fois, d'après la notice et les lemmes de Pappus, et conformément au sentiment de B. Simson sur la forme des énoncés de ces propositions» (Париж, 1860)
- XI и XII книги «Элементов» Евклида «םדילקא», в переводе Нахмана–Гирша Линдера, издание Давида Фризенгаузена (Житомир, 1875)
- «Euclidis Opera Omnia»:«Elementa», «Data», «Optica» на греческом, «реконструированные» с рукописей датским филологом Иоганном Людвигом Гейбергом (Johan Ludvig Heiberg, 1854–1928), с добавлением комментаторов Евклида на латинском и санскрите, изданные им в девяти томах (Lipsiae, 1883–88), на это издание опираются современные переводы «Начал» Евклида
Издания «Начал» Евклида на русском языке
- «Эвклидовы элементы, из двенадцати нефтоновых книг выбранные, и в осьмь книг чрез профессора мафематики Андрея Фархварсона сокращенныя», перевёл с латинского Иван Петрович Сатаров (СПб, 1739)
- «Елементы геометрии в 8 книгах», перевёл с французского Николай Гавилович Курганов (СПб, 1769)
- «Евклидовых стихий осмь книг, а именно: первая, вторая, третья, четвертая, пятая, шестая, одиннадцатая и двенадцатая. Переведены с греческого и поправлены», перевели с греческого Прохор Игнатьевич Суворов и Василий Никитич Никитин (СПб, 1784, в 1789 были добавлены книги XIII, XIV)
- «Евклидовых Начал осемь книг, содержащие в себе основания геометрии», перевод с греческого Фомы Ивановича Петрушевского (СПб, 1819)
- «Евклидовых Начал три книги: седьмая, осьмая и девятая, содержащие общую теорию чисел древних геометров», перевод с греческого Фомы Ивановича Петрушевского (СПб, 1835)
- «Восемь книг геометрии Эвклида. Переведено с немецкого издания доктора Гартвига воспитанниками Александровского Кременчугского реального училища Немировским и Бергером, под руководством Директора училища» (Кременчуг: типография Германа Розенталя, 1877)
- «Начала Евклида с пояснительным введением и толкованиями», вольный перевод, возможно, с латинского издания Р. Симсона 1723 года, Михаила Егоровича Ващенко–Захарченко, опущены арифметические книги VII–IX, а во введении изложена неевклидова геометрия (Киев, 1880)
- «Начала Евклида», перевод с греческого Дмитрия Дмитриевича Мордухай–Болтовского (Москва–Ленинград, книги I–VI — 1948; книги VII–X — 1949; книги XI–XV — 1950)
Продолжатели Евклида
Несколько математических проектов прямо указывают на свою связь с замыслом «Начал» математики Евклида:
- «Математические начала натуральной философии» («Philosophiae Naturalis Principia Mathematica», 1686) англичанина Исаака Ньютона
- «Начала геометрии» («Éléments de géométrie», 12 исправленных изданий, 1794—1823) француза А.–М. Лежандра
- «О началах геометрии» (1829—1830) и «Новые начала геометрии с полной теорией параллельных линий» (1835—1838) россиянина Н.И. Лобачевского
- «Основные законы арифметики» («Grundgesetze der Arithmetik: eine logisch–mathematische Untersuchung über den Begriff der Zahl», 1884) немца Г. Фреге
- «Основания геометрии» («Grundlagen der Geometrie», 1899) немца Д. Гильберта
- «Принципы математики» («Principia Mathematica», 1910—1913) англичан А.Н. Уайтхеда и Б. Рассела
- «Основания математики» («Grundlagen der Mathematik», 1934—1939) немца Д. Гильберта и швейцарца П. Бернайса
- «Элементы математики» («Éléments de mathématique», 1939—2016) французов Н. Бурбаки
- «Основания алгебраической геометрии» («Éléments de Géométrie Algébrique», ÉGA, 1960—1967) космополита А. Гротендика и француза Ж. Дьедонне
Мнения и анекдоты
- «... по отношению к сочинениям гуманитарного характера мы можем либо прямо указать предполагаемого автора, либо, по крайней мере, очертить круг людей, вполне способных им быть по их образованию, культуре и литературному дарованию. Совсем иначе дело обстоит, скажем, с Евклидом. Кто из ученых средневековья мог бы претендовать на эту роль? Вот что пишет по этому поводу Морозов: «Учёный, переписывая с дополнениями книгу дня себя, писал на ней совершенно справедливо то имя. которым она была помечена до него. «Геометрия Евклида», — отмечал он, — умолчав о том, что сам прибавил две–три теоремы от себя и лучше обосновал ту или другую из старых. Так он давал повод и последующему копиисту своей рукописи добавить две-три теоремы, сохранив за учебником прежнее имя. И вот, с течением веков, небольшой десяток теорем, который мог действительно быть собранным человеком этого имени (имя Евклид значит — хорошо одетый), превращался в большую и хорошо развитую во всех своих деталях книгу. А последующий учёный, упустивший из виду этот вековой процесс улучшения, начинал приписывать все такое коллективное творчество одному древнему гиганту геометрической науки и вместе с тем определять ложно высокий уровень познания в очень древние времена. На деле же вся книга представляла сумму познаний целого исторического периода до тех пор, когда печатный станок впервые повсюду распространил её и указал время и место её первого издания» («Христос», Т. 4.— М–Л.: ГИЗ, 1928, стр. 174–175). Добавим, что «Евклид» может означать также «хорошо переплетённый». Описанный механизм бессознательного коллективного творчества хорошо объясняет происхождение таких всеобъемлющих трактатов, как «Альмагест» Птолемея или «Начала» Евклида, и тот факт, что ссылки на них были возможны задолго до окончательного оформления их текста. Он не предполагает никакого явного обмана и мистификационных устремлений со стороны авторов и издателей, хотя возможность эта отнюдь не может быть исключена. Вместе с тем правила издания «древних» текстов были на заре книгопечатания явно отличны от современных. Как показывает пример, скажем, «Альмагеста», редакторы и издатели окончательного текста, не колеблясь, вносили в него поправки и дополнения, соответствующие последнему слову науки, никак это специально не оговаривая. Не потому ли «переводу» научных книг часто предшествовал «дурной перевод», не содержащий этих поправок и отражающий предыдущий этап развития науки?» (М.М. Постников «Критическое исследование хронологии древнего мира. I т.», §4)
- «О Эвклиде нам известно чуть больше, чем о Гомере. Он родился в Александрии около 325 года до Р. Х. и умер около 265 года до Р. Х. Сказав это, я с неудовольствием чувствую, что мне тут же надо бы взять свои слова назад. Идея, согласно которой Эвклид действительно существовал и был единственным автором «Начал»,— это только одна из трёх теорий. Вторая состоит в том, что он существовал, но не писал «Начала» — по крайней мере не писал их сам. Он мог возглавлять группу математиков, создавших «Начала» коллективно. Суть третьей теории — более спорной, но всё ещё лежащей в рамках возможного — в том, что такая группа существовала, но сильно смахивала на группу математиков — по бóльшей части французов и по бóльшей части молодых,— писавших в середине двадцатого столетия под именем Николя Бурбаки. Так что «Эвклид» может оказаться коллективным псевдонимом. Тем не менее наиболее убедительная версия, похоже, состоит в том, что Эвклид всё же существовал и что это был один человек, который сам и написал «Начала». Это не означает, что Эвклид сам открыл всё математическое содержание, которое вы найдёте на страницах его книги. ...» (И. Стюарт «Истина и красота: Всемирная история симметрии»,— М.: Астрель: CORPUS, 2010, стр. 47)
В историко–математическом сочинении «Eléments d'histoire des mathématiques» 1960 года Н. Бурбаки (основным автором текста, по–видимому, был Ж.А.Э. Дьедонне, 1906—1992) написали об истинных создателях «Начал» Евклида — математиках XV—XVII вв., а также их работе, следующее:
- «При таком взгляде на математику аксиомы не подвергались сомнению и не обсуждались, так же как и правила вывода; единственное, что предоставлялось каждому исследователю в зависимости от его склонности, это право либо рассуждать «по образцу древних», либо дать свободу своей интуиции. Выбор точки отправления также зависел от индивидуального вкуса, в результате чего появляются многочисленные «издания» Евклида, в которых самым странным образом искажена прочно сработанная логика «Начал»;...» («Очерки по истории математики»,— М.: КомКнига, 2007, стр. 22)
Американский математик Роберт Рот Столл (Robert Roth Stoll, 1915—1991, выпускник Йельского университета, США, 1943) в учебнике для студентов Оберлинского колледжа «Sets, logic, and axiomatic theories» (1961) изложил своё ошибочное понимание логического строения «Начал» Евклида (цитирование по русскому переводу этой книги):
- ««Начала» построены следующим образом. Сначала даются определения (по всей вероятности, считавшиеся Евклидом удовлетворительными) некоторых первичных терминов, таких, как точка, прямая и плоскость. Затем описываются различные свойства этих первичных терминов (некоторые из этих описаний Евклид называл аксиомами, другие — постулатами). Очевидно, утверждение о наличии этих свойств воспринимались как истинные на основании смысла предложенных определений рассматриваемых терминов. Далее, с помощью первичных терминов определялись некоторые другие понятия, а из аксиом и постулатов выводидись логическим путём описания новых свойств, называемые теоремами.» (Столл Р.Р. «Множества. Логика. Аксиоматические теории»,— М.: Просвещение, 1968, стр. 139–140)
Французский популяризатор математики Микаэль Лонэ в книге «Большой роман о математике» (Mickaël Launay «Le grand roman des maths: De la préhistoire à nos jours») сообщает своё мнение об Евклиде:
- «О жизни Евклида не сохранилось такого большого количества информации, как о Фалесе или Пифагоре. По одним данным, он жил где–то в районе Александрии. По другим — по аналогии с Пифагором, некоторые историки предполагают, что это вымышленное имя, под которым скрывается наследие нескольких учёных. Наверняка это нельзя определить.» (стр. 84)
См. также
Литература
- «Энциклопедический словарь Брокгауза и Ефрона, в 86 томах»,— СПб, 1890–1907
- Бородин А.И., Бугай А.С. «Биографический словарь деятелей в области математики. Под ред. И.И. Гихмана»,— Киев: Радянська школа, 1979, 607 с. (перевод с украинского)
- Носовский Г.В., Фоменко А.Т. «Царь Славян»,— СПб.: Нева, 2004, 640 с.
- Хониат, Никита «История, начинающаяся с царствования Иоанна Комнина. Том 2». Серия: Византийская историческая б–ка,— Рязань: Александрия, 2003
- «Начала Евклида, книги I–VI»,— М.–Л.: ОГИЗ, 1948, 447 с.
- «Начала Евклида, книги VII–X»,— М.–Л.: ОГИЗ, 1949, 511 с.
- «Начала Евклида, книги XI–XV»,— М.–Л.: ОГИЗ, 1950, 331 с.
- Диоген Лаэртский «О жизни, учениях и изречениях знаменитых философов»,– М.: Мысль, 1986
- Глухов А.Г. «Книги, пронизывающие века»,– К.: Радянська школа, 1979, 152 с.
- «Новый энциклопедический словарь»,— М.: Большая Российская энциклопедия, РИПОЛ КЛАССИК, 2002, 1456 с.
- Кымпан Ф. «История числа π»,— М.: Наука, 1971, 216 с.
- Folkerts M. «Euclid in Medieval Europe»,— München, 1989
- Постников М.М. «Критическое исследование хронологии древнего мира. В 3–х томах»,— М.: Крафт+Леан, 2000 (написана в 1978), 448+400+400 сс.
- Стюарт И. «Истина и красота: Всемирная история симметрии»,— М.: Астрель: CORPUS, 2010, 461 с.
Ссылки
- Эвклид «Начала», восемь книг. Книги 1–6, 11, 12. (1819)
- Первое печатное издание Евклида, 1482 г.
- Рыбников К.А Русские издания «Начал» Евклида (библиографические заметки) // Успехи Математических Наук, 1941, вып. 9, с. 318–321
- «Euclidis Codex» на греческом языке, Bodleiana Bibliotheca
- Видеолекция профессора РАН А.И. Буфетова об Евклиде и Лобачевском


